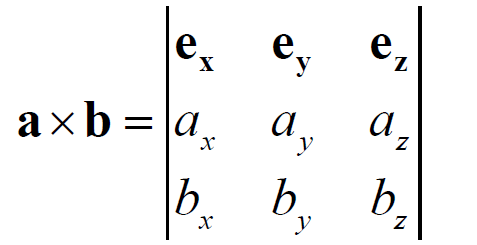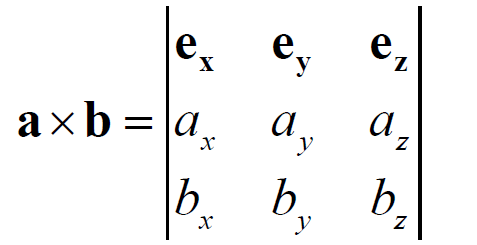第一章 矢量分析
标量场:ϕ(x,y,z,t)
矢量场:F(x,y,z)=Fx(x,y,z)ex+Fy(x,y,z)ey+Fz(x,y,z)ez
加法、减法、数乘、标量积(点乘)、矢量积(叉乘)
若c=a×b,则:∣c∣=∣a∣∣b∣sinθ ; a、b、c 三者方向遵循右手定则
注意: a×b=−b×a
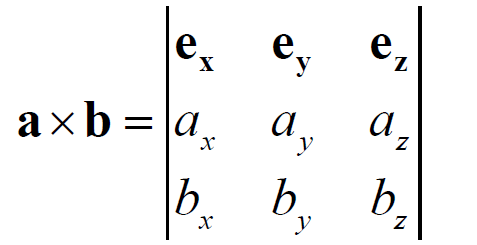
∫Sa⋅dS=∫Sa⋅n dS=∫Sa dS cosθ
div a=ΔV→0limΔV通量
div a=∂x∂ax+∂y∂ay+∂z∂az
定义哈密顿算符:∇=ex∂x∂+ey∂y∂+ez∂z∂ 则: div a=∇⋅a 两个向量和的散度:∇⋅(a+b)=∇⋅a+∇⋅b
∮sa⋅dS=∫V∇⋅a dV